|
| Other polyhedra | made of |
|---|---|
| Pyramid | triangles and square |
| Cube Octahedron | triangles and squares |
| Buckyball | pentagons and hexagons |
| Euler's formula | Useful links and books | |
| Glossary | Education ideas for using this webpage |
|
|
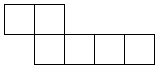
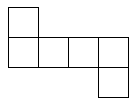
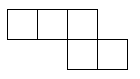
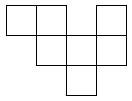
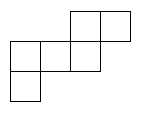
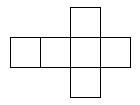
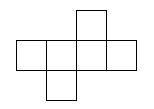
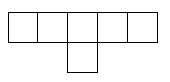
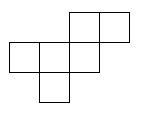
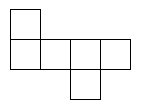
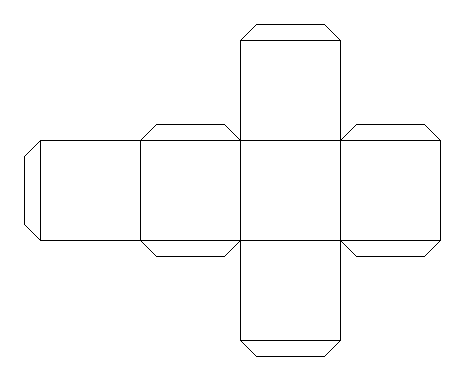Once you have chosen a net design, you need to draw it out. Here is one of them as an example. If you wish to print it out, right-click on it and choose 'Print picture'. You can choose another net from above. Scale it up to the size you want, and put a tab on every other edge for gluing it together. It's certainly possible to make a cube from ordinary paper, but it will be fragile. Don't sit on it by mistake! You can also use thin card. How about recycling packaging such as breakfast cereal packs? Draw out the design (if you haven't printed it) and cut it out carefully, using scissors that aren't blunt or covered with glue. Before gluing, it is important to fold the design. Use a ball-point pen to go over all lines in the design, including the tabs. You may find this easier before cutting it out, but I usually forget! The ball-point pen will make a mark so if you can find a ball point pen that doesn't work, that will be perfect. Press quite heavily with the point of the pen, but don't tear the paper. Now fold the paper to make right angles, and you will see the cube start to appear. It doesn't matter which way you fold the design. Once you have scored the edges with the ball-point pen, you will find it easy to fold it either way. Use small dabs of glue to stick it, or it will end up very messy.
Did you know that the opposite sides of a dice always add up to 7? If they don't on one of your dice, then it's not a proper dice!
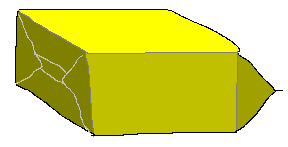Some cubic packaging is made of a single piece of card with some clever folding and gluing. Roll the paper or card into a cylinder and glue the edge to keep it like that. Put four folds in length-wise to make a square cross-section to the cylinder. Pinch one end and glue it across. Pinch a fold in to give it a sharp edge. Do the same to the other end. The corners of the ends will stick out. Fold them inwards. To open the carton, you unfold the ends, and snip a corner. The diagram shows one end with corners folded in, and the other with them unfolded.
It's easy to think of a cube as a very man-made shape, and that there are no cubes in nature. Well, you'd be wrong! On the left is a pyrite crystal. It is natural, not shaped by man, and it is definitely a cube. You might think that crystals are transparent and jewel-like, but there are many metallic crystals. You can see a mini-crystal starting to grow on the top at a different angle.
This model (right) was made from a kit with magnetic connections. Since it just shows the edges, you can see through the model, which means that you can count the vertices and edges easier. How many vertices (corners) and edges are there? See Euler's formula. I'm sorry if the model is a little wobbly. Squares don't make stable shapes, unlike triangles.
|
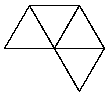
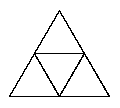
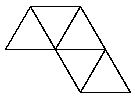
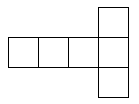
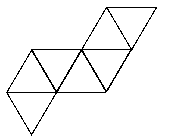
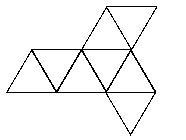
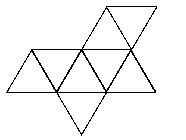
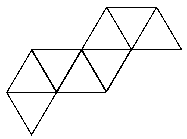
See the notes for the net of a cube to see how to print this net and make your own tetrahedron.
|
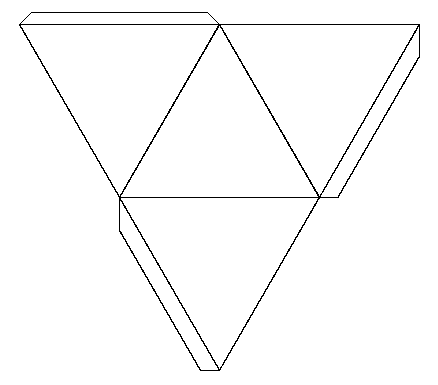
This model (right) was made from a kit with magnetic connections. Since it just shows the edges, you can see through the model, which means that you can count the vertices and edges easier. How many vertices (corners) and edges are there? See Euler's formula.
Tetrahedra are not very common. They do have one useful property; they are very stable. A caltrop is an unpleasant medieval weapon. It has four sharp points, arranged at the vertices (corners) of a tetrahedron. Whichever way you throw it, one point will always point straight up. Anyone treading on this will get a spike through their foot!
You can get tetrahedra packaging, usually for liquids such as fruit juice. These are made in a clever way, which you can try for yourself. Make a cylinder of paper and glue the edge down. Pinch one end, and glue that. Now pinch the other end in the opposite direction, and glue that. It will naturally form a tetrahedron, although you might need to play around with the dimensions of the cylinder to get a regular tetrahedron.
|
|
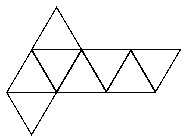
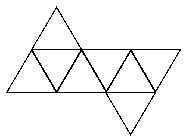
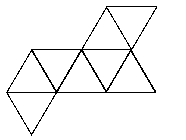
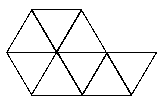
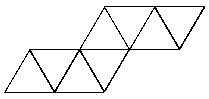
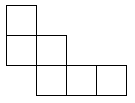
See the notes for the net of a cube to see how to print this net and make your own octahedron.
|
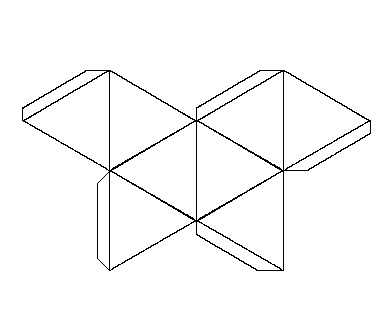
Octahedra happen in crystals as well as cubes. This is a natural spinel crystal. Spinels are red gem stones, often mistaken for rubies.
This model (left) was made from a kit with magnetic connections. Since it just shows the edges, you can see through the model, which means that you can count the vertices and edges easier. How many vertices (corners) and edges are there? See Euler's formula.
An octahedron can look different from different angles. It can look like two pyramids or, from the top, it can look like a star of David.
|
|
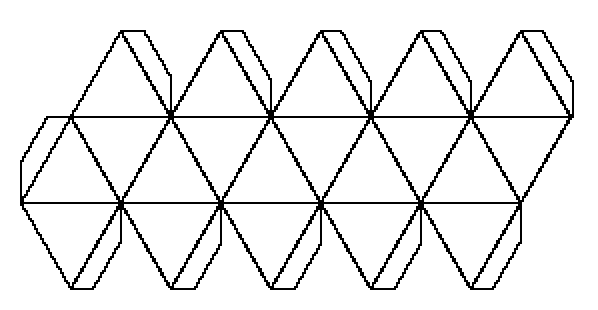
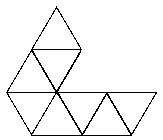
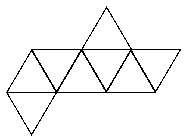
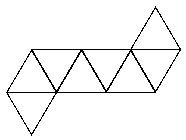
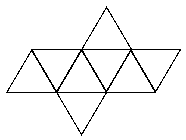
See the notes for the net of a cube to see how to print this net and make your own icosahedron.
You might like to think of a colour scheme for your finished shape. It's a lot easier if you colour it in before you stick it together, or even before you cut it out. Try to imagine what the finished shape will look like when colouring it in. You could try to draw lines that run over edges. That's easy if the faces are together in the net, less easy if there are gaps! Do you want straight lines or curvy ones? Can you draw a line which will end up going right round the shape? How about colouring all the bits near a point in the same colour? Then when you stick it together, you can see if your shape's design looks anything like you imagined it would! |
This model (right) was made from a kit with magnetic connections. Since it just shows the edges, you can see through the model, which means that you can count the vertices and edges easier. Unfortunately, since the icosahedron is quite complicated, one edge and one vertex(corner) is hidden, several more are hard to make out, and the shadows don't help! Still, you can guess, or perhaps you can make up your own model to count from. How many vertices (corners) and edges are there? See Euler's formula.
|
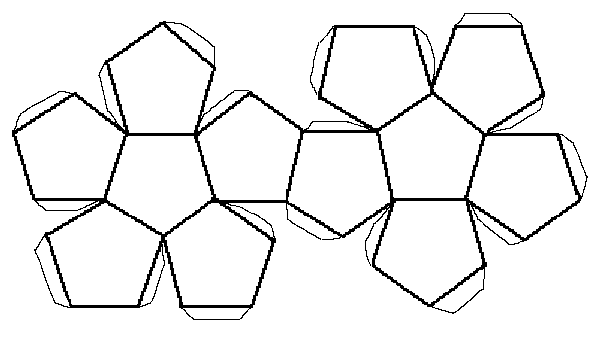
See the notes for the net of a cube to see how to print this net and make your own dodecahedron. I'm afraid that the tabs are not very neat on this diagram as they were free-drawn by mouse, which I find tricky. Still, it doesn't matter as they end up inside your finished shape.
Dodecahedra happen in crystals as well as cubes and octahedra. This is another natural pyrite crystal. It is not actually a regular dodecahedron, although it has 12 faces, each with 5 sides, but it is quite close..
|
Unfortunately, my magnetic kit didn't have enough connectors to make a dodecahedron, so here is a child's ball instead. You can't see through it, and I think it needs washing! You can count the faces from the net above. To get the edges, count the number of sides per face, and multiply that by the number of edges. But then remember that each edge is shared by two faces, so you need to divide by two. To get the vertices, count the corners of one face, multiple by the number of faces, and then divide by three, since there are three faces at each vertex. See Euler's formula for what to do with these numbers.
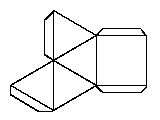
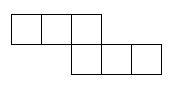
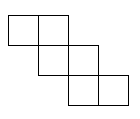
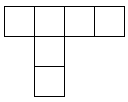
The regular pyramid is a tetrahedron, which is made entirely of triangles, even its base. However, the pyramids in Egypt at Giza are square pyramids. Here is a net to make one for yourself. It is not a regular polyhedron, since it uses a square as well as triangles.
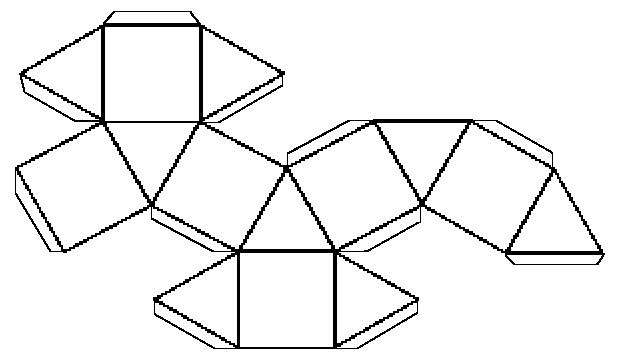
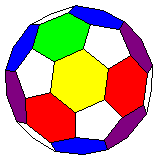
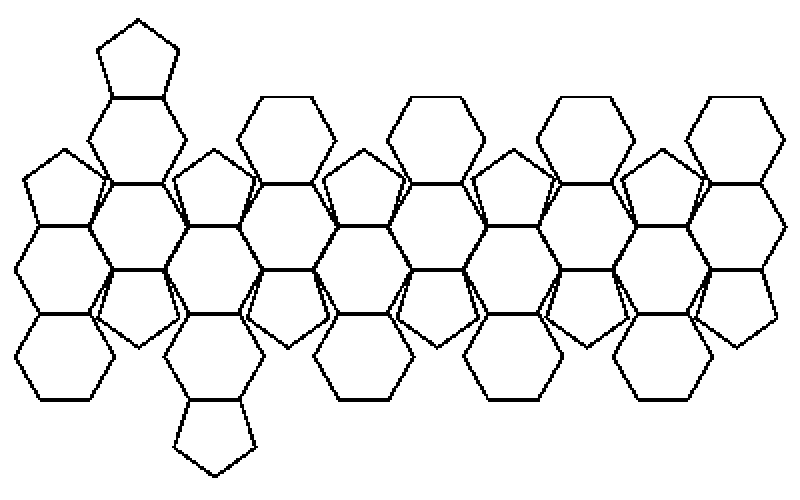
There is a story that a scientist discovered what the molecule of a new form of carbon looked like. He found that it was an interesting shape, a bit like a ball, but made of hexagons and pentagons arranged in a regular pattern. He was very excited and rang up a friend who was a mathematician to boast of this new shape that he'd found. The mathematician told him to look at a soccer ball! Even footballers can't get away from mathematics. This shape is called a buckyball after Richard Buckminster Fuller, who invented the geodesic dome.
| Polyhedron | Faces | Vertices (corners) | Vertices + Faces | Edges |
|---|---|---|---|---|
| Cube | 6 | 8 | 14 | 12 |
| Tetrahedron | 4 | 4 | 8 | 6 |
| Octahedron | 8 | 6 | 14 | 12 |
| Icosahedron | 20 | 12 | 32 | 30 |
| Dodecahedron | 12 | 20 | 32 | 30 |
|
|
© Jo Edkins 2004